एक समद्विबाहु त्रिकोण के कोणों को कैसे प्राप्त करें?

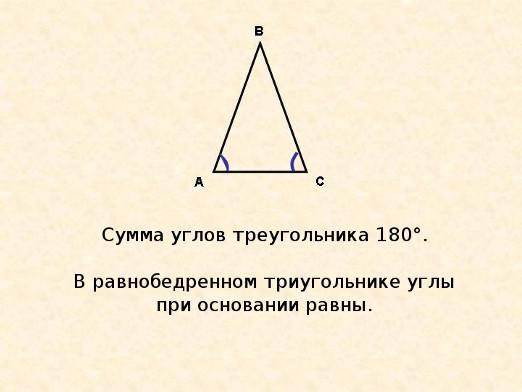
एक समद्विबाहु त्रिकोण एक हैसरल कोण के तीन कोण और तीन तरफ समूहीकृत त्रिभुज के कोणों को कैसे पता चले, इससे पहले कि आप इस ज्यामितीय आंकड़े के गुणों को जानना चाहते हैं

एक समद्विबाहु त्रिकोण की गुण

आइए एक समद्विबाहु त्रिकोण के गुणों पर विचार करें।

एक समद्विबाहु त्रिकोण में, दोनों पक्ष समान हैं। तीसरी पार्टी का आधार है।
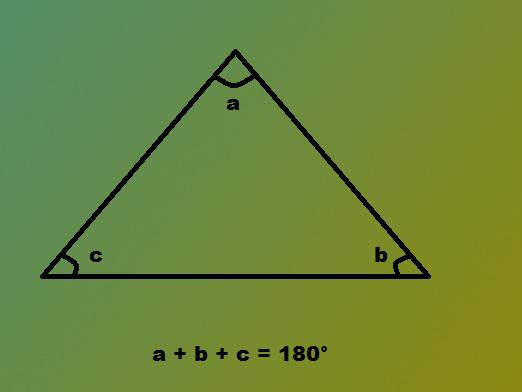
ऐसे त्रिकोण के आधार पर कोण समान हैं।
द्विभाजक, मध्यक और ऊँचाई को कोनों से ज्यामितीय आकृति के विपरीत दिशा में खींची गई है, वह भी बराबर है।
द्विभाजक, ऊपरी कोने से औसत और ऊंचाई समद्विबाहु त्रिकोण के आधार पर होता है।
यदि आप एक समद्विबाहु त्रिभुज के अंदर एक वृत्त लिखते हैं, और इस तरह के एक आंकड़े के आसपास इसका वर्णन करते हैं, तो उनके केंद्र एक ही पंक्ति पर झूठ होंगे।
आधार पर कोनों केवल तेज हो सकते हैं

इस प्रकार, यदि दो कोण एक त्रिकोण में बराबर हैं, और इसकी ऊंचाई एक माध्य और एक द्विभाजक के साथ मेल खाती है, यह समद्विबाहु है यह एक समद्विबाहु त्रिकोण का मुख्य लक्षण है

अब, विचार करें कि कोणों को कैसे ढूंढेंएक समद्विबाहु त्रिकोण अगर ऐसा त्रिकोण आयताकार भी है, तो इसके दो कोणों को ढूंढना मुश्किल नहीं है, इसलिए वे हमेशा 45 डिग्री के बराबर होंगे, जो गुणों और एक समद्विबाहु त्रिभुज के संकेतों से निम्नानुसार होगा।

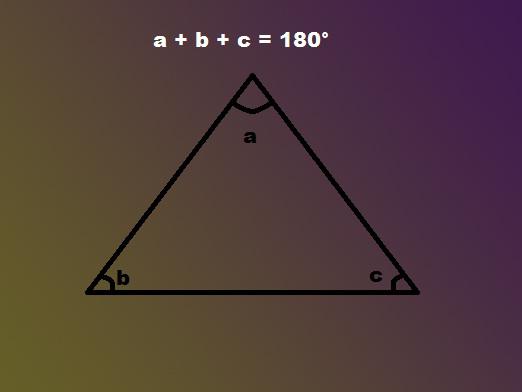
कोणों में से एक को जानने के लिए, आप हमेशा गणना कर सकते हैंकी जरूरत है। उदाहरण के लिए, आधार पर कोण को α के अक्षर से चिह्नित किया जाएगा, चित्रा के शीर्ष पर कोण को अक्षर β से चिह्नित किया जाएगा। इसलिए कोण α के बराबर होगा: (π - β) / 2, जहां π एक स्थिरांक है
कोणों को आर्सेन्स से भी गणना की जा सकती है इस प्रयोजन के लिए यह एक त्रिज्या जो बड़े अक्षर आर से दर्शाया जाता है तो फिर साथ सर्कल के चारों ओर इस तरह के एक त्रिकोण का वर्णन करने के लिए आवश्यक है, कोण α = arcsin (एक / 2R), और कोण β = arcsin (ख / 2R), जहां ए और बी एक त्रिभुज की भुजाओं हैं।

समस्या के समाधान का उदाहरण

यदि समझा जाता है कि समद्विबाहु त्रिभुज में कोणों को ढूंढना आवश्यक है, तो उसके आधार पर कोण आधार के विपरीत कोण से 15 डिग्री अधिक है।

समाधान: विपरीत कोण β को निरूपित करें, फिर नीचे का कोण होगा: β + 15. चूंकि त्रिकोण में योग हमेशा 180 डिग्री होता है, हम पाते हैं:

β + 2 बी (बीओ +15) = 180;

β + 2 β + 30 = 180;

3 β = 180-30;

3 β = 150;

β = 50

इसलिए, नीचे के कोण 50 डिग्री हैं, औरतो दूसरे दो कोण 65 डिग्री प्रत्येक के बराबर हैं अब आप नियमों को जानते हैं कि एक समद्विबाहु त्रिभुज के कोणों को कैसे ढूँढें। हम आपको सभी गणना में शुभकामनाएं देते हैं!