एक समद्विबाहु त्रिकोण की गुण

एक त्रिकोण जिसका दो तरफ के बीच बराबर हैसमस्थानिक कहा जाता है इन पक्षों को पार्श्व कहा जाता है, और तीसरी तरफ आधार कहा जाता है इस अनुच्छेद में, हम आपको एक समद्विबाहु त्रिकोण के गुणों के बारे में बताएंगे।

प्रमेय 1

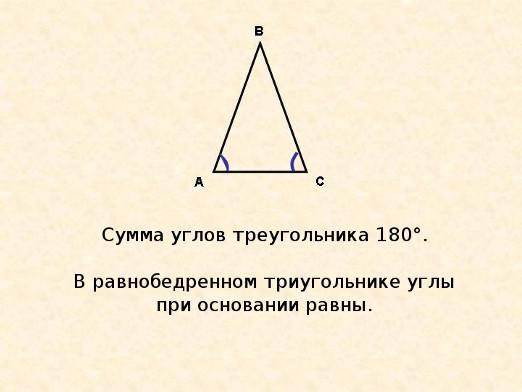
एक समद्विबाहु त्रिकोण के आधार के पास के कोण एक दूसरे के बराबर हैं

प्रमेय का सबूत

मान लीजिए कि हमारे पास एक समद्विबाहु त्रिभुज हैएबीसी, जिसका आधार एबी है चलो त्रिकोण बीएसी को देखें इन त्रिकोण, पहले चिन्ह द्वारा, एक दूसरे के बराबर हैं तो यह है, क्योंकि बीसी = एसी, एसी = बीसी, एसीबी = एसीबी का कोण इसलिए यह इस प्रकार है कि कोण बीएसी = कोण एबीसी, क्योंकि ये हमारे बराबर त्रिकोण के कोने हैं। यहां एक समद्विबाहु त्रिभुज के कोणों की संपत्ति है

प्रमेय 2

समद्विबाहु त्रिकोण में मध्य, जो उसके आधार पर किया गया था, ऊंचाई और बिस्केट्रिक्स भी है

प्रमेय का सबूत

मान लीजिए कि हमारे पास एक समद्विबाहु त्रिभुज हैएबीसी, जिसका आधार एबी है, और सीडी हम अपने आधार के लिए आयोजित औसत दर्जे का है। त्रिकोण एसीडी और बीसीडी में, कोण सीएडी = सीबीडी कोण, एक समद्विबाहु त्रिकोण के आधार पर इसी कोण के रूप में (प्रमेय 1)। और पक्ष एसी = पक्ष बीसी (एक समद्विबाहु त्रिकोण की परिभाषा के अनुसार) साइड एडी = पक्ष बीडी, बिंदु डी के बाद से खंड एबी को बराबर भागों में बांटता है। इसका अर्थ है कि त्रिभुज एसीडी = त्रिकोण बीसीडी

इन त्रिकोणों की समानता से हमारे पास हैंकोनों की समानता यही है, कोण एसीडी = बीसीडी के कोने और एडीसी एडीसी = बीडीसी के कोने यह समानता 1 से चलता है कि सीडी एक द्विभाजक है और कोण एडीसी और कोण BDC आसन्न कोण हैं, और यह समानता 2 से होता है कि वे दोनों सीधे हैं। यह पता चला है कि सीडी एक त्रिकोण की ऊंचाई है यह एक समद्विबाहु त्रिकोण के मध्य की संपत्ति है

और अब एक समद्विबाहु त्रिकोण के संकेत के बारे में थोड़ा।

प्रमेय 3

यदि त्रिकोण में दो कोण एक दूसरे के बराबर होते हैं, तो ऐसे त्रिकोण समद्विबाहु होते हैं

प्रमेय का सबूत

मान लीजिए हमारे पास त्रिकोण एबीसी है, जिसमेंकोण सीएबी = सीएबी के कोने त्रिभुज एबीसी = त्रिभुज बीएसी त्रिकोण के बीच समानता के दूसरे संकेत द्वारा। तो यह है, क्योंकि एबी = बीए; कोण CBA = कोण CAB, कोण CAB = कोण CBA त्रिभुज की इस समानता से हमारे पास त्रिभुज के समान पक्ष की समानता है - एसी = बीसी फिर यह पता चला है कि त्रिकोण एबीसी समद्विबाहु है

प्रमेय 4

यदि कोई भी त्रिभुज में इसकी मध्य भी इसकी ऊंचाई है, तो ऐसे त्रिकोण समद्विबाहु है

प्रमेय का सबूत

त्रिभुज एबीसी में, हम सीडी के मध्य खींचे। यह ऊंचाई भी होगी आयताकार त्रिभुज एसीडी = आयताकार त्रिभुज बीसीडी, क्योंकि सीडी उनके लिए सामान्य है, और कैथोड एडी = बीडी। यह निम्नानुसार है कि उनके कर्ण का एक दूसरे के बराबर है, जैसा कि समान त्रिकोण के इसी भाग के रूप में। इसका अर्थ है कि एबी = बीसी

प्रमेय 5

यदि त्रिभुज के तीनों पक्ष दूसरे त्रिकोण के तीनों तरफ बराबर होते हैं, तो ये त्रिकोण समान होते हैं

प्रमेय का सबूत

मान लीजिए कि हमारे पास त्रिभुज एबीसी और त्रिकोण A1B1C1 है, जैसे पक्ष एबी = ए 1 बी 1, एसी = ए 1 सी 1, बीसी = बी 1 सी 1। हम इस प्रमेय के सबूत पर विरोधाभास से विचार करते हैं।

मान लीजिए कि ये त्रिकोण बीच के बराबर नहीं हैंअपने आप से इसलिए हमारे पास यह है कि कोण बीएसी कोण B1A1C1 के बराबर नहीं है, कोण एबीसी कोण A1B1C1 के बराबर नहीं है, कोण ACB उसी समय कोण A1C1B1 के बराबर नहीं है अन्यथा, ये त्रिकोण उपरोक्त फीचर के अनुसार समान होंगे।

मान लें कि त्रिकोण A1B1C2 = त्रिभुजएबीसी। त्रिभुज में, शीर्ष सी 2 एक आधा विमान में लाइन A1B1 के सापेक्ष शीर्ष सी 1 के साथ स्थित है। हमने मान लिया है कि सी 2 और सी 1 कोने में नहीं है। मान लीजिए कि बिंदु डी सी 1 सी 2 के मध्य बिंदु है। तो हमारे पास समद्विबाहु त्रिभुज बी 1 सी 1 सी 2 और ए 1 सी 1 सी 2 है, जो एक सामान्य आधार सी 1 सी 2 है। यह पता चला है कि उनके मध्य B1D और A1D भी उनकी ऊंचाई हैं इसका मतलब है कि सीधी रेखा B1D और सीधी रेखा A1D सीधी रेखा सी 1 सी 2 के लिए लंबवत हैं।

बी 1 डी और ए 1 डी के पास अलग-अलग बिंदु बी 1 और ए 1 हैं, और, तदनुसार, मेल नहीं खा सकते हैं। लेकिन वास्तव में, सी 1 सी 2 के बिंदु डी के माध्यम से, हम इसे एक सीधी रेखा को सीधा रेखा से आकर्षित कर सकते हैं। हमारे पास एक विरोधाभास है

अब आप जानते हैं कि एक समद्विबाहु त्रिकोण के गुण क्या हैं!