पिरामिड की सतह क्षेत्र कैसे प्राप्त करें?

हम किस आंकड़े को पिरामिड कहते हैं? सबसे पहले, यह एक बहुरूपदर्शक है दूसरे, एक मनमाना बहुभुज इस बहुध्रुव के आधार पर स्थित है, और पिरामिड (पार्श्व वाले चेहरे) के पक्ष में आवश्यक रूप से त्रिकोण का एक रूप है, जो एक सामान्य शिखर पर केंद्रित होता है। अब, शब्द का पता लगाना, हम यह पता लगाएंगे कि पिरामिड की सतह क्षेत्र कैसे खोजना है।

यह स्पष्ट है कि इस तरह के ज्यामितीय निकाय के सतह क्षेत्र में बेस के क्षेत्रफल और इसकी संपूर्ण पार्श्व सतह शामिल होगी।

पिरामिड के आधार के क्षेत्र की गणना

गणना सूत्र की पसंद अंतर्निहित के रूप पर निर्भर करता हैहमारे बहुभुज पिरामिड के आधार पर यह सही हो सकता है, वह यह है कि, समान लंबाई के पक्ष के साथ, या गलत। चलो दोनों वेरिएंट पर विचार करें।

नीचे एक नियमित बहुभुज है

विद्यालय के पाठ्यक्रम से हम जानते हैं:

• वर्ग का वर्ग अपने पक्ष की लंबाई के बराबर होगा, स्क्वेर्ड;
• एक समभुज त्रिभुज का क्षेत्र उसके पक्ष के वर्ग के बराबर होता है जिसे 4 से विभाजित किया जाता है और तीन के वर्गमूल से गुणा किया जाता है।

लेकिन गणना के लिए एक सामान्य सूत्र भी हैकिसी भी नियमित बहुभुज (एसएन) के क्षेत्र में: इस बहुभुज (पी) के परिधि में उस वृत्त में त्रिज्या के दायरे से गुणा करें, और उसके बाद परिणाम दो में विभाजित करें: Sn = 1 / 2P * r

नीचे एक अनियमित बहुभुज है

अपने क्षेत्र को खोजने की योजना है,पहले, त्रिकोण में पूरे बहुभुज विभाजित सूत्र के अनुसार उनमें से प्रत्येक के क्षेत्रफल की गणना करने के लिए: 1/2 ए * ज (जहां एक - त्रिकोण के आधार, ज - आधार ऊंचाई को कम कर दिया जाता है), सभी परिणाम जोड़ें।

पिरामिड का भूतल क्षेत्र

अब पिरामिड की पार्श्व सतह के क्षेत्र की गणना करें, अर्थात। अपने सभी पार्श्व पक्षों के क्षेत्रों का योग वहाँ भी 2 विकल्प हैं

1. हमारे पास एक मनमाना पिरामिड है, अर्थात। ऐसे में, जो एक अनियमित बहुभुज है। तब हमें अलग-अलग प्रत्येक चेहरे के क्षेत्र की गणना करनी चाहिए और परिणाम जोड़ना चाहिए। चूंकि परिभाषा के अनुसार पिरामिड के पक्ष केवल त्रिकोण हो सकते हैं, परिकलन से ऊपर के सूत्र का अनुसरण करता है: S = 1 / 2a * h।
2. हमारा पिरामिड सही हो, यानी, इसके आधार में एक नियमित बहुभुज है, और पिरामिड के शीर्ष पर प्रक्षेपण उसके केंद्र में है फिर, पार्श्व सतह (एसबी) के क्षेत्र की गणना करने के लिए, पार्श्व पक्ष की ऊंचाई (एच) द्वारा बहुभुज-आधार (पी) के परिधि के आधा उत्पाद को खोजने के लिए पर्याप्त है (सभी चेहरे के लिए समान): एसबी = 1/2 पी * एच बहुभुज की परिधि सभी तरफ की लंबाई जोड़कर निर्धारित की जाती है।

नियमित पिरामिड का कुल सतह क्षेत्र पूरे बेसल सतह के क्षेत्र के साथ अपने बेस के क्षेत्र को जोड़कर पाया जाता है।

उदाहरण

उदाहरण के लिए, हम कई पिरामिड के बीजीय रूप से सतह के क्षेत्रों की गणना करते हैं।

त्रिकोणीय पिरामिड का सतह क्षेत्र

ऐसे पिरामिड के आधार पर एक त्रिकोण है। सूत्र के अनुसार = 1/2 ए * एच हम बेस के क्षेत्र को खोजते हैं। एक ही सूत्र का उपयोग पिरामिड के प्रत्येक चेहरे के क्षेत्र को खोजने के लिए किया जाता है, जिसमें त्रिकोणीय आकृति भी होती है, और हम 3 क्षेत्रों: एस 1, एस 2 और एस 3 प्राप्त करते हैं। पिरामिड की पार्श्व सतह का क्षेत्रफल सभी क्षेत्रों का योग है: एसबी = एस 1 + एस 2 + एस 3। पक्षों और आधार के क्षेत्रों को जोड़ना, हम वांछित पिरामिड का कुल सतह क्षेत्र प्राप्त करते हैं: एसएन = एस 0 + एसबी।

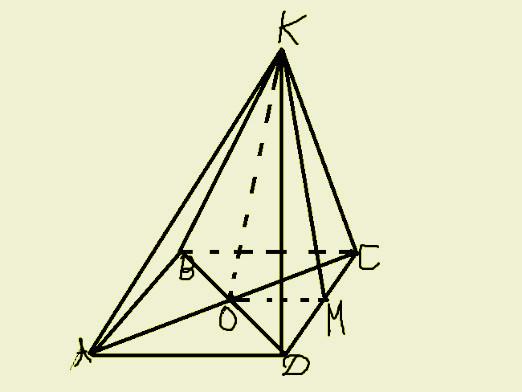
चतुर्भुज पिरामिड का सतह क्षेत्र

पार्श्व सतह का क्षेत्र 4-एक्स की राशि हैशर्तें: एसबी = एस 1 + एस 2 + एस 3 + एस 4, जिनमें से प्रत्येक को त्रिकोण के क्षेत्र के सूत्र द्वारा गणना की जाती है। और आधार क्षेत्र को चतुर्भुज - सही या गलत के आकार के आधार पर खोजा होगा। पिरामिड का कुल सतह क्षेत्र फिर से निर्दिष्ट क्षेत्र को जोड़कर और निर्दिष्ट पिरामिड का कुल क्षेत्रफल जोड़कर प्राप्त किया जाएगा।