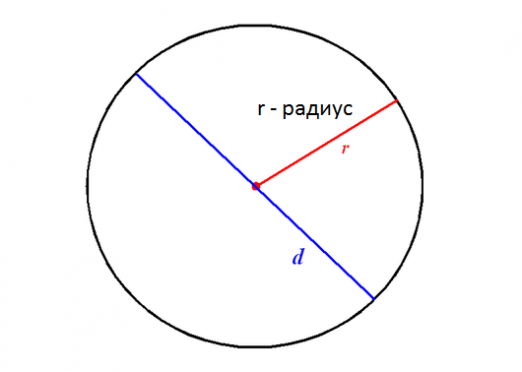
परिबद्ध चक्र के त्रिज्या कैसे खोजते हैं?

अक्सर ज्यामिति में एक का सामना करना पड़ता हैसर्किल सर्किल और उनके त्रिज्या यह एक सरल प्रश्न की ओर जाता है: परिबद्ध मंडल के त्रिज्या कैसे खोजता है? बहुभुज के चारों ओर वर्णित परिवृत्त एक बहुभुज के कोने के माध्यम से गुजर रहा है। एक सर्कल एक विमान में अंक (ज्यामितीय) का स्थान है जो विमान के एक बिंदु (केंद्र) से समानांतर होता है।

त्रिकोण के परिमाणबद्ध चक्र के त्रिज्या

त्रिकोण के परिवृत्त के त्रिज्या को खोजने के लिए, हम निर्धारित करने के लिए एक सरल सूत्र का उपयोग करते हैं:

• पी = (1/2) (x + y + z), जिसे हम (*) द्वारा दर्शाते हैं
• आर = xyz / (4 वी (पी (पी-एक्स) (पी-वाई) (पी-जेड))), जिसे हम (**) द्वारा दर्शाते हैं, जहां x, y, z त्रिकोण के पक्ष हैं; त्रिभुज के परिमाणबद्ध चक्र के त्रिज्या है।

नियमित बहुभुज के परिमाणबद्ध चक्र के त्रिज्या

एक नियमित बहुभुज बराबर पक्षों और कोणों वाला एक बहुभुज है। और एक नियमित एन-गोन के आसन्न कोने के बीच के कोण के बराबर है:

बीओए = एक्स = 360 डिग्री / एन, जहां बीओए त्रिकोण है, एक्स इसकी आधार की लंबाई है, और एन एक नियमित बहुभुज के पक्ष की संख्या है।

हम त्रिभुज बीओए अलग से बनाते हैं उसके बारे में हम जानते हैं:

1. यह समद्विबाहु है;
2. त्रिभुज बीओए के कूल्हों को भी नियमित एन-गोन के परिमाणबद्ध चक्र की त्रिज्या होती है;
3. त्रिभुज बीओए के आधार "एक्स" की लंबाई मूल नियमित बहुभुज की तरफ है।
4. त्रिज्या आर के बीच का कोण, जिसे हमने पहले सूत्र (**) से गणना की थी।

सबसे पहले, ऊंचाई को कम करने के लिए आवश्यक है और आयताकार त्रिभुज पर विचार करें, जो हमें मिला। कोण के त्रिकोणमितीय कार्यों की सहायता से (इस मामले में तीव्र) हम प्राप्त करते हैं:

पाप (360 ° / 2 एन) = एक्स / 2 आर, जिसमें से हम एक नियमित एन-गोन के परिमाणबद्ध चक्र के उचित त्रिज्या के सूत्र प्राप्त करते हैं:

आर = एक्स / (2 सिन (360 ° 2 एन)), आर नियमित एन-गोन के परिमाणबद्ध चक्र के त्रिज्या है, एक्स नियमित बहुभुज का पक्ष है, और n नियमित बहुभुज के पक्ष की संख्या है।