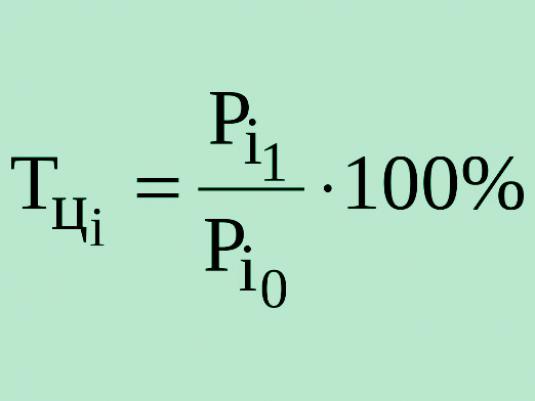क्यूब की गणना कैसे करें?
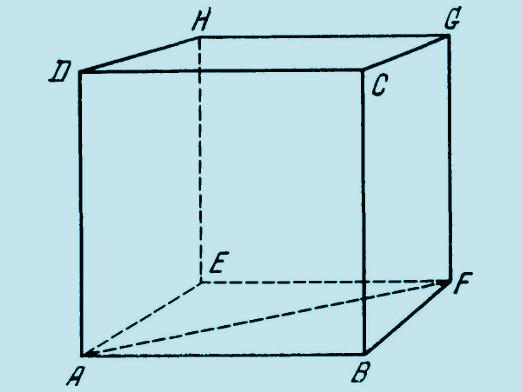
सबसे पहले, यह समझने के लिए कि क्षेत्र की गणना कैसे करेंक्यूब, आपको यह पता होना चाहिए कि किस प्रकार की आकृति है, कौन सी विशेषताएँ और गुण हैं चूंकि क्यूब क्या है और इसके मुख्य घटक क्या हैं, यह जानने के कारण, यह ज्यामितीय आंकड़ा की गणना करना आसान होगा। इसलिए, एक क्यूब एक नियमित बहुध्रुव है, और उसके प्रत्येक चेहरे का एक वर्ग है। क्यूब के किनारों में छः हैं। इसके अलावा, निजी घन मामलों रहे हैं: - यहाँ एक स्पष्ट समानांतर चतुर्भुज एक प्रिज्म और समानांतर खात आकार या polyhedrons डेटा, अन्य घटकों, अर्थात् है, चश्मे उनके चेहरे बराबर बहुभुज, समानांतर चतुर्भुज, और बॉक्स के लिए के रूप में जोड़ती है। क्यूब की गणना करने से पहले, हम इसके गुणों से निपटेंगे:
- क्यूब के क्रॉस-सेक्शन हेक्सागोन हैं।
- क्यूब का विकर्ण एक ऐसा खंड है, जो दो कोने से जोड़ता है, और वे घन के केंद्र में बदले में सममित होते हैं।
- हम इस आंकड़े को हल करने के लिए मुख्य सूत्र देते हैं:
- क्यूब का क्षेत्र - 6 ए2 ;
- मात्रा है - ए3 ;
- क्यूब में लिखे गए क्षेत्र के त्रिज्या 1/2 * a;
- वर्णित क्षेत्र के त्रिज्या - 3 से 2 विभाजित और "a" द्वारा गुणा के साथ रूट।
क्यूब की गणना के लिए निर्देश
के बाद से सवाल हमारे साथ है: कैसे घन की गणना करने के, चलो कैसे बाहर ज्यामितीय आकृति की गणना ले जाने के लिए पर कदम निर्देश के द्वारा कदम हैं:
- हमें पता चला कि क्या हैघन, इसके मुख्य घटकों की गणना करने के लिए इसमें क्या विशेषताएं हैं, सूत्र, गणनाओं को स्वीकार करना आवश्यक है सबसे पहले, ध्यान दें कि आपके पास कौन सी जानकारी है (पक्षों के आयाम, विकर्ण की लंबाई), अगर कोई जानकारी नहीं है, तो इसे काफी सरल किया जाना चाहिए - क्यूब के किसी भी किनारे का नाम "a"। आगे गणना में, इस पत्र मूल्य से शुरू करें।
- इसके बाद, अपनी गणना कताई शुरू करें, जैसे किधागा की उलझन यदि क्यूब के एक किनारे "a" है, तो कोई भी अन्य "a" भी है। इसके बाद आपको चेहरे के क्षेत्र की गणना करने की आवश्यकता है, और चेहरे एक समान सामान्य वर्ग है - सभी के लिए जाने वाले वर्ग का वर्ग2। विकर्ण घन भी मापना मुश्किल नहीं है, के साथपायथागॉरियन प्रमेय का उपयोग करना, जो "ए" के बराबर होता है, दो के वर्गमूल से गुणा करता है। याद रखें कि मोटे तौर पर एक घन बोल रहा है, यह एक बड़ा वर्ग है, जिसकी गणना आपको लगभग सब कुछ मिलेगा।
- अब हम अन्य गणनाओं में आगे बढ़ सकते हैं, उदाहरण के लिए, क्यूब के क्षेत्र, जो कि जैसा हमने पहले ही उल्लिखित किया है, 6 ए है2। यही है, एक चेहरे का क्षेत्र जानने - हम क्षेत्र और पूरे घन पाएंगे लगभग उसी तरह, हम घन की मात्रा पा सकते हैं इस तथ्य से कार्य करना कि मात्रा एक के बराबर है3, तब सभी पक्ष "a" के मान के बराबर हैं, जिसका अर्थ है कि क्यूब आसानी से नहीं मिल सकता है।
तो यहाँ एक सरल तरीका है, आपने सीखा है कि आपको किसी भी क्यूब की गणना करने के लिए कौन-से क्रिया करने की आवश्यकता है। कोशिश करो, प्रयोग करें!