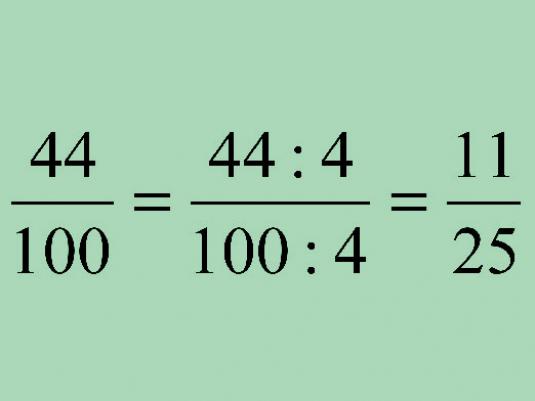अंश कैसे मिलेंगे?

गणित विज्ञान की रानी है उसकी महानता अनंत है, लेकिन उसकी शक्ति महान है अन्य सभी विज्ञान गणितीय परिणामों पर भरोसा करते हैं। चाहे वह भौतिकी, रसायन विज्ञान, जीव विज्ञान, और यहां तक कि भाषाशास्त्र भी हो।
जैसा कि घर ईंटों से बना है, इसलिए प्रत्येक कार्य में छोटे उपकार्य हैं। और छोटे को हल करने के लिए सीखने से, आप अधिक जटिल समस्याओं को हल करने के लिए सीख सकते हैं।
आज हम विश्लेषण करेंगे कि अंश कैसे मिलेंगे। यूनानियों ने पूर्णांक के समतुल्य लंबाई की अवधारणा को प्रस्तुत करने के बाद, ग्रीस में भिन्नता की अवधारणा उत्पन्न हुई थी। इसके बाद, हमें एक अवधारणा की आवश्यकता थी जो लंबाई का एक हिस्सा व्यक्त करती थी, उदाहरण के लिए आधे, लंबाई का एक तिहाई तो अंश की अवधारणा दिखाई दी
तर्कसंगत संख्याओं का सेट, प्रपत्र m / n में दर्शाए गए संख्याओं का सेट है, जहां m, n पूर्णांक हैं संख्या m / n को एक साधारण अंश कहा जाता है, जहां मी एक अंश है, और n एक छेद है, n ≠ 0
यदि n = 〖10〗 ^ k, k = 1,2, ..., तो ऐसे अंश को दशमलव कहा जाता है और 0,0..0m के रूप में लिखा जाता है, अल्पविराम के -1 होने के बाद शून्य की संख्या के साथ।
एक संख्या को समग्र कहा जाता है, अगर 1 और इसके अलावा अन्य डिवाइजर भी हैं।
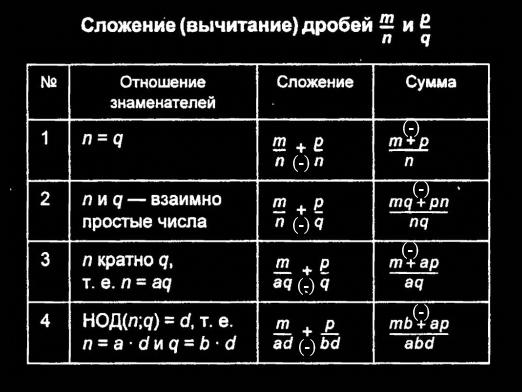
बुनियादी संचालन
भिन्नताओं को जोड़ा जा सकता है, घटाया जा सकता है, गुणा किया जा सकता है, विभाजित किया जाता है, एक शक्ति में उठाया जाता है। ये संचालन मूल हैं उदाहरणों में,
हम सरल से जटिल से आगे बढ़ेंगे, उदाहरण के द्वारा दिखाएंगे कि इन या अन्य कार्यों को कैसे ठीक किया जाता है।
एक अंश को कम कैसे करें
ऐसा करने के लिए, हमें प्रधान कारकों के द्वारा अंश और विभाजित करना होगा, यदि वे समग्र कारक हैं और आगे, यदि ये सरल कारकों का मिलान हुआ है, तो उन्हें हटाएं।
प्रमुख कारकों की अनुपस्थिति में, अंश को अपूरणीय कहा जाता है। उदाहरण के लिए, 85/65 = (17 * 5) / (13 * 5) = 17/13
संख्या से एक अंश कैसे प्राप्त करें
नंबर एक निश्चित लंबाई होना चाहिए। एक अंश अनिवार्य रूप से इस लंबाई का एक हिस्सा है, इसलिए पूर्णांक भाग को खोजने के लिए, संख्या से अंश गुणा करें। उदाहरण के लिए, 2/3 का 27 = 27 * 2/3 = 27/3 * 2 = 18
एक अंश से एक अंश कैसे प्राप्त करें
वास्तव में, यह एक साधारण गुणन प्रक्रिया है, एक अंश का एक अंश खोजने के लिए, आप केवल 2 अंशों को बढ़ाते हैं उदाहरण के लिए, 2/3 और 13/17: 2/3 * 13/17 = 26/51
अंशों की विखंडन
अंशों को विभाजित करते समय ए / बी, सी / डी, विभाजक सी / डी को डी / सी और गुणा के रूप में प्रस्तुत किया जा सकता है, और फिर कट कर सकते हैं। उदाहरण के लिए, 27/17 9/34 = 27/17 * 34/9 = 2 * 3 = 6
यह भी याद रखना आवश्यक है कि जब जटिल हल करनाउदाहरणों को एक समाधान एल्गोरिथम के साथ आने की जरूरत है। विभेद में बदलाव के साथ विभाजन को बदलना आवश्यक हो सकता है, गुणा करना और उसी संख्या से विभाजन करना संभव है। ऐसे सरल पर्याप्त निर्देश उदाहरणों को सुलझाने में मदद करेंगे।
एक उदाहरण के रूप में, शास्त्रीय पाठ ले लोकार्य। जिस गोदाम पर 150 टन ईंधन तेल चोरी हुआ 2/3 था चोरी किए गए हिस्सों को 5/17 और 12/17 के अनुपात में भागों में वितरित किया गया था, बाद के प्रसंस्करण के लिए ले जाया गया था। शेष ईंधन तेल प्रसंस्करण के लिए ले जाया गया था। कितना ईंधन तेल पुनर्नवीनीकरण किया गया है?
150 * 2/3 * 12/17 + 150 * (1-2/3) = 150 * 41/51
अंशों के लिए कार्य स्कूल अंकगणित का आधार है। वे प्रकृति में जटिल नहीं हैं, लेकिन इसे मेहनती और चौकस होने की आवश्यकता है। यदि ये स्थितियां पूरी होती हैं, तो परिणाम बहुत लंबा नहीं होगा